subir
Python-backpropagation
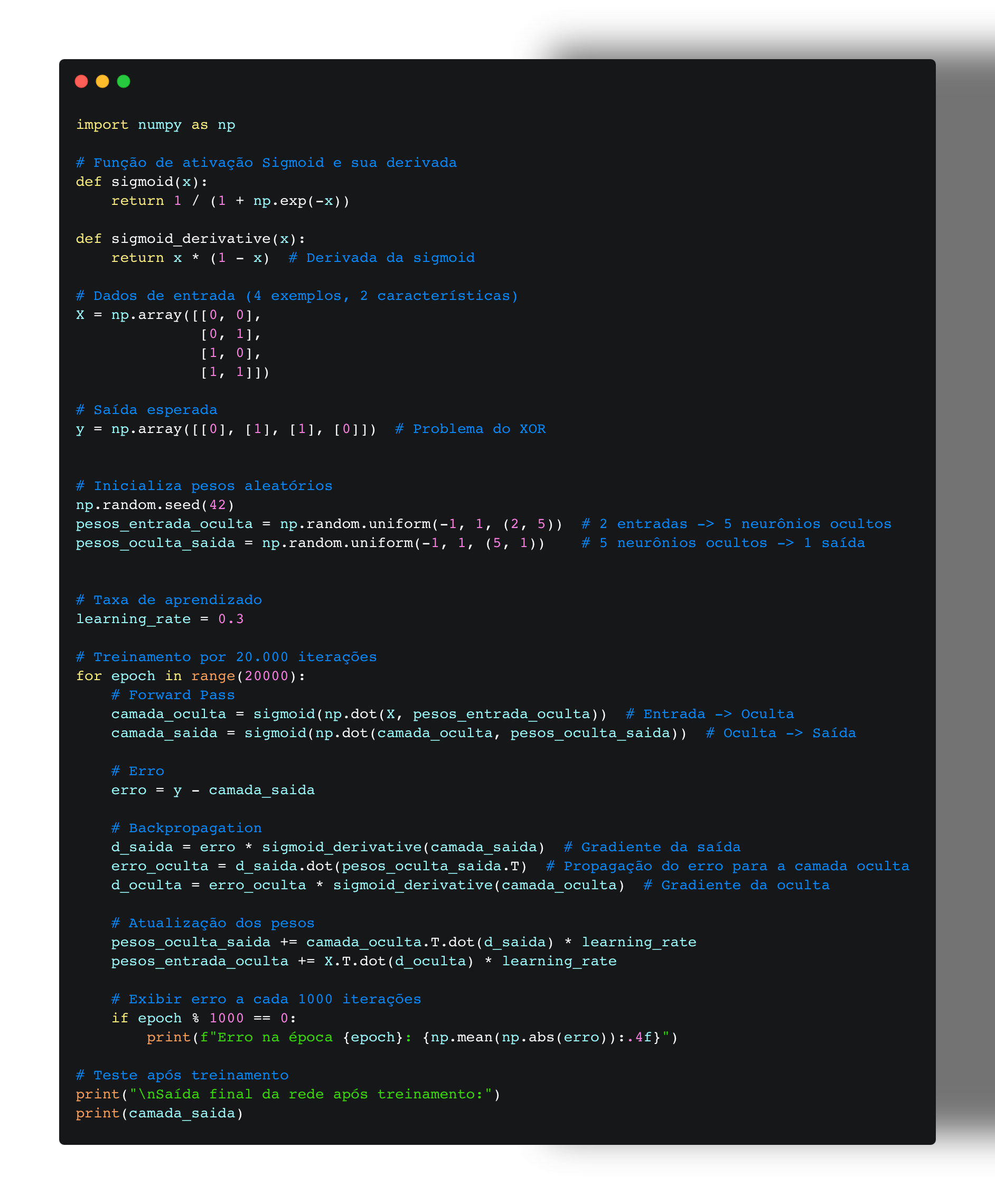
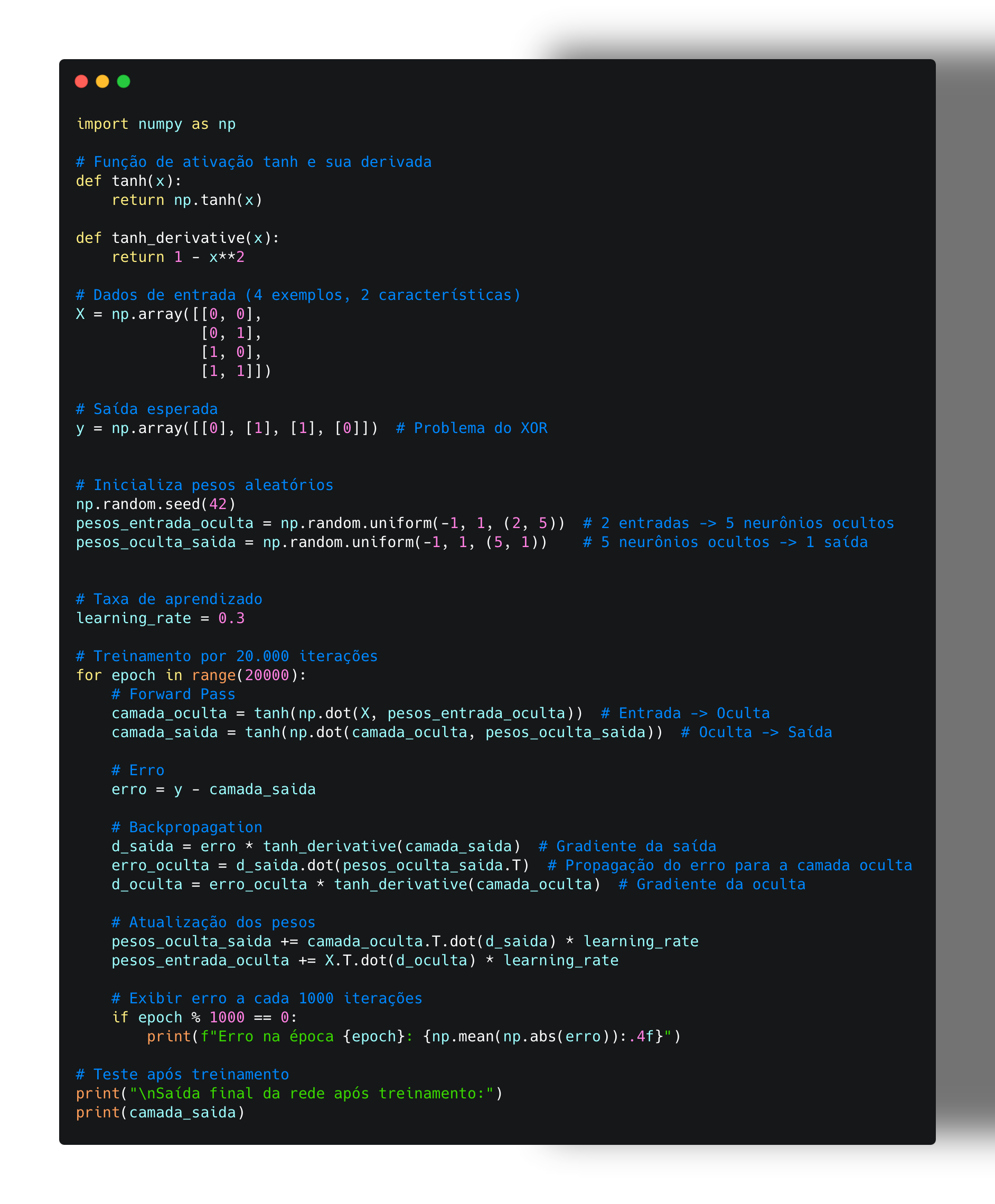
Python-backpropagation é uma implementação do algoritmo de backpropagation em Python, utilizado em redes neurais para treinamento supervisionado.
Principais Funcionalidades
Função Sigmoide
A função sigmoide é utilizada para transformar qualquer valor em um valor entre 0 e 1, sendo útil para problemas de classificação binária.
Função Tanh
A função tangente hiperbólica é utilizada para transformar qualquer valor em um valor entre -1 e 1, sendo útil para problemas de regressão.
Como Contribuir
Contribuições são sempre bem-vindas! Veja como você pode ajudar:
Reportar Bugs
Encontrou um problema? Abra uma issue no GitHub com detalhes sobre o bug.
Sugerir Funcionalidades
Tem uma ideia interessante? Compartilhe suas sugestões de melhorias.
Contribuir com Código
Fork o projeto, faça suas alterações e envie um pull request.
Apoio Financeiro
Se você gostou do projeto Python-backpropagation e está satisfeito com o funcionamento, considere fazer uma doação para apoiar o desenvolvimento contínuo do projeto. Pix: andersoncomercial@pm.me